Increasing 200 day moving averages

I did a quick study of what happens if you look at whether the 200 day moving average is increasing or not. I used the same asset classes and methodology as this which through February of this year showed a return of 11.98% (6.82% std, .875 Sharpe). I looked at three improvements which probably do not have different enough results to tell a priori which is better.

1. 1. If the 200 day moving average is increasing a buy signal is generated, invest in cash otherwise.
2. 2. Entry order is only generated when the price is greater than the 200 day MA, only exit if the 200 MA decreases.
3. 3. Same entry order, but exit if below 200 day MA and 200 day MA decreases.

The first shows a return of 12.5% (6.9% std, .947 Sharpe), the second has a return of 12.8% (6.9% std, .975 Sharpe), and the final has a 12.4% return (6.6% std, .961 Sharpe). For the first one, the bond portfolio underperforms relative to the classical TAA model from Faber. In the second, the real estate portfolio underperforms. However, this is also dependent on the time period. Over the whole period the real estate underperforms, but since 1995, the second method produced strong returns in real estate (though the third method does better). The second method has the benefit of simplicity and surprisingly is in the market more often than the traditional TAA method.

I had originally assumed it would be in less. I wanted a method that would use the same entry and get you out quicker when the market begins to tank, but it appears that the benefit comes from keeping you in the market longer (roughly 70% of the months that are different are from the second method having a buy rather than a sell) and these months, particularly for commodities and stocks, generate strong returns and the handful of months avoided have relatively mixed returns. However, when they are down, they are down pretty significantly (real estate is an anomaly that acts opposite both effects). I was also surprised to find out that on average the TAA method generates on average 50 entry or exit signals per asset class whereas the second method generates about 45.

In conclusion, the TAA model can benefit by being in the market longer and not necessarily trying to avoid more periods.

TAA and avoiding pullbacks

I should probably be studying, but this didn't take me that long to work out and was pretty interesting.

This could be considered another extension of the tactical asset allocation system developed by Mebane Faber that I have blogged about several times. The original strategy is to invest in five asset classes (US bonds, US stocks, Foreign stocks, Commodities, Real Estate) when they are greater than their 200 day moving average and commercial paper otherwise.

I modified the system slightly, maintaining the 200 day moving average requirement, but I added an additional constraint: it could not be the case that it was above the 5 month (4 and 6 have similar results) moving average and the return over the previous month was negative. The point of this was to take into account periods being overbought and then getting back in quickly. The periods above the five month that have negative prior month returns have very poor risk to reward ratios, most significantly for stocks and REITs. So making this simple addition can take a system with an 11.9% historical return with 6.8% standard deviation (.867 Sharpe at 6%) to 11.8% with 5.68% standard deviation (1.026 Sharpe). Though there is not a statistically significant difference in means, there is a significant difference in standard deviations according to an F test.

Not only is this improvement a significant, easy to implement improvement, but it is based on logic. Most trends do not continue up continuously. There tend to be pull backs. This strategy maintains the idea that the trend is your friend and attempts to stay out of a pull back if it happens two months in a row.

Note: the portfolio leveraged 50% has a 14% return with 8.5% standard deviation compared to 13.5% with 9% standard deviation for the original version. The best benefit in reducing standard deviation is in keeping the risk to reward statistics strong when using leverage.

TAA update

I probably will not be posting that often for the next three weeks or so. I have the level 2 C.F.A. coming up and I have got to hit the books.

Anyway, unless there is a correction, May will show a signal to invest in equities according to the TAA model. I was interested in the returns in time periods when the previous signal was to not invest and the following month closed above the 200 day moving average. By comparison, the excess monthly TAA return is 5.16% historically with a 6.94% standard deviation (12% normally) and5.8% excess return (13.76% standard deviation) for the S&P500 timing model. When there are two consecutive months of buy signals, the similar statistics are 6.25% return (13.48% standard deviation). For the S&P500 when there is a sell signal in the month prior and a buy signal in the present month, the average excess return has been .09% with a 12.81% standard deviation. However, if you look at all of the assets, commodities and foreign stocks have very strong returns that keep the overall strategy strong. Excluding the S&P500 dates until there are two buy signals slightly reduces the standard deviation while keeping returns positive, though it doesn't appear to be statistically significant.

For the 24 times since 1974 that if you bought the S&P500 at the beginning of the month when price crossed above the 10 month SMA, you probably wouldn't have any return, but the standard deviation of equities.

OverBought/OverSold part 2

Regarding yesterday's post with OverBought and OverSold indicators, I combined that with the TAA model from before (5 asset classes, buy above 200 day, invest in Commercial paper otherwise). I just wanted to add in RSI since that had a tendency to be most effective (can't use lower bollinger band since already out, not enough data for stochastics). I started with the method from yesterday (only invest when RSI is less than 75) which works very well with equities, but this method does not work as well with the other asset classes and it significantly underperforms as a diversified strategy. However, it remains significant for equities, so I will leave it in place for them. EAFE benefits from staying away when there is an RSI less than 50, but the other asset classes are already out of the market enough due to the TAA that it really doesn't improve their situation that much (25 results in no change for any of them) and the change just for commodities won't change the results significantly (statistically or economically). Ignoring the OverBought RSI figure for everything except equities also improves returns (different time periods are slightly improved by reducing them to 98 or 95, but it is not statistically or economically significant).

In other words, what is true for yesterday was likely true just for the S&P500 and not something applicable to a diversified strategy. However, just including it for equities can raise the Sharpe ratio from .88 to 1 over the entire time period and from .94 to .99 since 1990. Not a statistically significant difference for the overall strategy, but since it is statistically significant for the underlying, it might be worth considering an addition. A strategy that avoids situations where the monthly return is greater than the 2 (or 2.5 or 3) stdev Bollinger Band does not improve returns overall.

OverBought/OverSold

One of my interests is looking into ways to improve investing returns. I decided to look just at the S&P500 on a monthly basis since 1967. Mebane Faber has noted that the returns to a 10 month simple moving average strategy earns significant returns. In this sample, the returns are statistically significant with a 12.2% return (13.5% standard deviation) compared to a statistically insignificant 5.8% (18.3%) when below. I wanted to test three common OverBought/OverSold indicators on a monthly basis and then check to see if they would be any benefit when combined with the 200 day strategy.

The three indicators I used were Relative Strength Index, Slow Stochastic, and Bollinger Bands. I would imagine that most people who would come to this site has heard of these concepts (which you can google if my explanations aren't good enough), but I'll explain their basic concepts anyway. The Relative Strength Index scales the ratio of the size of recent up moves to down moves. If there are more up moves, then the ratio will tick up which is then scaled from 0 to 100. The %K fast stochastic indicator measures where the most recent close is relative to the range the stock has been trading in. If it is trading near recent highs, then it will be closer to 100 and closer to 0 when trading near lows. Slow Stochastic is a 3 month MA of the fast. Bollinger Bands measure 2 (or n) standard deviations away from the moving average. For all of these, I use ten months as the initial range. I'm only able to do the slow stochastic since 1988 since I couldn't get highs or lows before then.

The biggest problem with these is that compared to the 10 month strategy, these have relatively few occurrences. So instead of being concerned with Sharpe ratios, I'm mostly concerned with statistical significance.

The results are that few of the indicators result in statistically significant returns. Overbought/oversold points on the 2 stdev Bollinger Bands are not significant with almost zero return when greater than the 2 and too few observations when less than the -2 (though that return is about 20% annualized). With breakpoints at 20 and 80, the oversold RSI is not statistically significant, but the Overbought is statistically significant in the positive direction. In other words, when the RSI is greater than 80, the market generally keeps going up. However, at the 90 breakpoint, it is no longer statistically significant. Combining those two signals (greater than 80, less than 90 (or 95) is statistically significant and occurs in about 72 months (14.5% of total). This indicates to me that the RSI does work as a momentum indicator and as an OverBought/OverSold indicator. Finally, the Slow Stochastic with 20 or 80 is significant (though both are positive). There are only five cases where the Slow Stochastic was under 20 (including March) and the average return in the next month has been 5.4% (this April did not disappoint). Increasing the low breakpoint up to 25 still gives significance and increasing the high breakpoint all the way up to 95 still shows significance with positive returns (I expected negative). This would indicate to me that Stochastics are not particularly good as OverBought/OverSold indicators on a monthly basis. However, it is really the most extreme readings that really generate statistically insignificant results. So it might make sense to look at a stochastic of 98, but a stochastic of 85 or 90 is probably more indicative of momentum than anything else.

So how would an investor incorporate these into a strategy? In general, you would want to stay away from situations where you do not generate statistically significant returns and invest when they are. Including the strategy when the slow stochastic is greater 80 or 90 combined with the 200 day MA does not change returns. The 200 day covers the momentum effect already. Avoiding the situations where it is above 98 does not result in a statistically significant difference between the two results. The below 20 or 25 is not statistically significant either. However, both of those two increase the Sharpe ratio of the strategy (note I use since 1988 for this part, but since '67 for the rest).

For the Bollinger Bands, you may as well ignore the OverSold indication since it always comes when you are out anyway due to the 200 day. The OverBought indication increases the Sharp ratio, but its inclusion is not statistically significant compared to the 10month SMA strategy.

What is true for the OverSold in Bollinger Bands, is also true for the RSI. The 200 day already gets you out of the market. Even the best combinations of the OverBought indicator (noted before at 80 and 90) do not improve significantly on the 200 day MA. However, if you reduce the break down to 75 and do not invest when the momentum is greater than that, then you will significantly increase returns at the 10% level. I just kind of pulled that number out of the air so I was surprised it works and am more afraid that it was a bit of curve fitting. The only problem is that if you are an investor looking for total returns, you will reduce the months of investing by almost 50%. Even still, though, if you include the risk-free return, then the historic returns for this strategy are at 11.5% (10.7% SMA) with a standard deviation of 8.1%(11.6% SMA). That ratio of return to risk is consistent over multiple time periods. The ratio is also fairly consistent going down through 70 (and below, though the returns suffer since you are in that many fewer days). The good thing about the RSI is that it is easily incorporated into other strategies since it only uses closing prices.

One additional improvement (that could be some curve fitting action) would be to make three requirements for a position, the first is SMA or below 25 on the stochastic, the second is RSI less than 75, and the third that the stochastic is not greater than 95. This return is significantly greater than the original SMA almost at the 2.5% level. After incorporating the risk-free return, the Sharpe ratio is .71 vs. .63 for only the RSI requirement, and finally .43 for the SMA. I plan on backtesting the TAA strategy with the RSI requirement, but I cannot backtest the complete method since I don't have high/low information for total return indices on bonds and REITs. ETFs have the information, but the time frame is smaller which makes comparisons difficult (though implementation is still possible).

In conclusion, OverBought and OverSold indicators can have some value in pointing out time periods to avoid (or get in), but they seem to have the most value when used in conjunction with each other. There are many dangers with curve fitting when using this kind of analysis, so the general rule is to keep it simple stupid and test a strategy that works on one set of data on other sets and look for some kind of consistency in the returns.

Commodities and Countries Update

I added in the combined the j/k momentum model and the TAA model for the commodity and currency strategies I described yesterday(before it was only TAA, but I know follow the guidelines described in this post). The results confirmed the reasoning in yesterday's post. Commodities historically (tested since 83) do not have a very powerful momentum strategy. However, the j/k strategy with countries and the TAA model combined outperforms using the TAA model individually on each country. However, the TAA model generates very few signals and would be better for a longer-term investor. The j/k model (with j=4, k=2, and investing in the top 25%) with TAA overlay has a CAGR/Stdev of 2.18 (CAGR: 9.5%) compared to .99 (CAGR: 12.4%) for the EAFE TAA strategy. The EAFE without currencies in the TAA has a Sharpe of about 1 and 1.14 with them. Those increase to 1.07 and 1.23 (1.04 and 1.19 for yesterday's). However, regressing the new excess returns on the individual TAA excess returns does not generate significant alpha (annualized 26 bps), but the Beta is only .81. Unlike yesterday's strategy (ex-currencies), this strategy does have a significant alpha (at 10%) of 50 basis points relative to the original TAA strategy with a Beta of .78 (it improves to significant at 5% with 55 basis points with the currencies relative to TAA with currencies compared to 30 bps for the strategy yesterday).

* 50% decreases the Sharpe of the foreign strategy by themselves, but increases the Sharpe of the OVERALL strategy, I just wanted to be consistent with previous posts

addendum: I should note that the returns to this strategy are over a long period of time, particularly since the currency strategy benefits from high interest rates. The Sharpe ratios come down significantly over the past ten years compared to the past thirty years. Since the strategy has maintained a more constant growth path (ie not the early/mid 80s), the country strategy improves the Sharpe from .83 to .96 for the TAA strategy (individual country TAA is .93). However, the inclusion of the currency strategy has a smaller effect (I don't take into account the declining value of the dollar on any assets besides currencies, so this could be understated) increasing the Sharpe ratio by .04-.05. It seems that compared to the 50% momentum strategy over the past ten years, the EAFE has outperformed historically so that the momentum strategy is relatively constant, but the EAFE outperforms. (.4 10 year Sharpe vs. .1 30 year) in the past few years. I'm not sure how long the EAFE will continue to outperform, but I would prefer the less volatile Sharpe ratio. Right now my thinking is that after taking into account the depreciation of all of these assets in dollar terms, the best cash strategy would be the currency strategy, but I'm not sure yet.

Commodities and Foreign Countries

Continuing on with my theme of finding ways to improve the TAA model (here, here, and here), I thought I would do some more research into a longer examination of a timing strategy, but breaking apart an index into its component parts. I don't use the momentum strategy described in my Component TAA, Part II post (noted above), but just the normal timing model after breaking apart the EAFE and GSCI into their components. The strategy is to go long the components above the 10 month SMA and be in cash otherwise, just like Mr. Faber's TAA strategy.

I'll start with the GSCI. I used data available from the Global Financial Database on Commodities futures since 1983 (except Natty Gas which is since 1990). Unfortunately, they didn't have all of the energy contracts and were missing a few of the other contracts. I kept each commodity subgroup (livestock, ag, energy, ind. metals, precious metals) the same weight and scaled up the components. I confirmed that this index has about a 94% correlation with the GSCI. I was a little disappointed with this figure (preferring higher than 97.5%), but I will make due with what I have. I tested just performing the timing on the sectors (since 91) and on the individual components (since 83). One thing is very clear, the GSCI is dominated by energy you cannot compare an equally weighted TAA strategy with the market-weighted portfolio in GSCI. If you compare the strategies, use weights close to GSCI.

With sectors and a buy and hold strategy, my returns are initially different than the GSCI, so I don't expect the best comparison for the timing, but with 94% correlation, I would expect similar trends. However, I found that the return/sd ratio increased for the GSCI strategy, but not the component strategy. Variance decreased, but returns decreased as well and the effect was not economically significant. On the other hand, the returns to the GSCI strategy are enhanced considerably. The returns and correlations are roughly the same if you break it down into all of the contracts weighted by what is in GSCI. I wouldn't be surprised if some of this result is due to the fact that many of these commodities contracts show considerable seasonal variation that cannot be reduced easily by using the 200 day MA the way that an equity indices returns are improved (they lack the seasonal variations) and that the aggregate figure trends better. A more complex strategy, such as taking advantage of contango or backwardation, might be more appropriate for the components of the GSCI. There are other indices that I could use to test this method since I didn't have all the contracts (I will use the CRB indices except energy which I will have to recreate).

Countries, on the other hand, do trend well and the timing strategy works very well on them. I used total return data and replicated the EAFE index since 1994 with a 99% correlation. Before that time period, I replaced the FTSE-100 with the All-Shares index and some other total return indices are used that don't have futures contracts for them.

(begin digression: I had to use alternative indices for some countries that didn't have total return indices for the whole period, however, the question is how the strategy improves on this Buy and Hold strategy and not necessarily on the EAFE. If it improves returns over a long period of time, you could reasonably assume that it would continue to outperform in the future with futures contracts available and that the returns that you have are highly correlated with what you would have had with futures contracts. The returns are probably slightly better since the indices used are all-share instead of focused, but you would also expect the variance to be higher, it is equivalent to using the Wilshire 5000 instead of S&P500: end digression).

I also didn't use all of the indices in the EAFE since some of them have very small weights and the countries don't have actively traded futures. The top 12 or so are good enough. In general the equal weighted strategy outperforms the EAFE weights (due to the 25% weight on Japan). The difference isn't large enough to concern ourselves about over the long-term (1.26 CAGR/STD vs. 1.25). Over the long-term, the buy and hold returns were different between the EAFE and weighing the individual components (since there are times when I don't have France or Singapore's total return indices), but again the comparison I want to make is between the trends and not the absolute levels. From 1970 to February of this year, the Buy and Hold for the EAFE had a CAGR/std ratio of .715 (CAGR=11.7%) and the component strategy was .82 (CAGR=13.1%). Overlaying the timing strategy increased the Sharpe ratio on the EAFE to .99 (CAGR=12.4%) and the component to 1.25 while increasing the return to 13.6%. Since 1988 (when I have data on France), the spread between the strategies has stayed strong although overall returns aren't as strong. The Buy and Hold on EAFE went from .43 to .64 and with the component strategy it went from .62 to .95.

The 6% Sharpe ratio of the original TAA strategy was about 1.0 (12.4% CAGR) since April of 1980 and 1.14 (12.3% CAGR) with a currencies strategy. Replacing the EAFE increases the Sharpe to roughly 1.04 (12.5% CAGR) in the original and 1.18 (12.4% CAGR). The excess returns show an insignificant alpha over the original TAA strategy, but with the currency strategy included there is a significant alpha of 30 bps which reduces to about 25 bps when currencies have a 3x weight (Sharpe of 1.31 vs. 1.27 originally).

Also note that this is a timing model just like the one before. There isn't the excessive trading costs of a momentum strategy. You would be in each country about 60-75% of the time and frequently for years at a time. Someone with a large account could use this strategy to help reduce risk while keeping returns constant (meaning more leverage could be used).

Currency Strategies

Just to note: compared to the previous post, this post looks into currencies with proper data and more importantly, accounts for interest rates.

There are four main sources of currency beta: value, momentum, carry, and volatility. Value is described as the PPP strategy, taking advantage of relative differences in long-term reversals to the mean of currencies with overvalued or undervalued currencies (on the basis on inflation and interest rates). Momentum is a trend-following strategy. Carry is investing in high interest rate countries and borrowing in low interest rate countries. A volatility strategy uses options on currencies and would be more exotic than a retail investor would want to use (and is most likely used to take into account exotic strategies a hedge fund manager uses and show that they are most likely just long/short volatility).

Well, I have been interesting in including the Beta of currencies in tactical asset allocation portfolios (see here for original post) and I wanted to experiment with these strategies. I generally am skeptical of the mean-reversion strategy since I've seen the charts of countries deviating from PPP estimates for decades. It's too hard to compare a basket of consumption goods between the countries to measure PPP accurately enough for me to be confident enough to invest using it. Volatility would also be too difficult to test and I've never traded currency options. It might be something to add in the future, but I'm guessing that strategy is too volatile for me...

So I set my eyes on the carry and momentum strategies. The carry strategy is particularly interesting to me since there already is an ETF which does that for you. DBV goes long the highest yielding currencies and short the lowest yielding ones to profit from the spread of the interest rates so long as exchange rates do not move very far. I replicated the strategy using all of the currencies that the ETF uses (and before the Euro I used France and Germany) going back to 1980 (when I could get decent interest rate data for some of the smaller countries). I replicated the DBV strategy as best as I could, except that I had to use some alternative interest rate data with longer histories instead of Libor (and then I continued to use that instead of switching to the country's interbank rates after the interbank data becomes available). I got a 95% correlation with the DBV since it has been in existence with a 10% return with a 7.8% standard deviation since 2000 (however, they report a cumulative return of 518% (14.67% annualized) since inception and I only showed 354% (8.5%), not sure how they account for the Euro, this could be the reason why). It's not perfect, but it's good enough (mine is crude since it may not always be market neutral b/c I'm lazy and don't plan to use it to invest with)

Taking the strategy further back (to 1980), there was a smaller return 6.3% (with 9% std) which could be attributable to wider (or more volatile) interest rate spreads during the 1980s which converged to roughly .4% in recent years. Ultimately the strategy has a very low correlation with the timing strategy that's been developed here and at WorldBeta and with the momentum strategy I will detail below. Also, based on my crude analysis, applying a 10 month moving average to this strategy increases the return:risk ratio from .694 to 1.15 (without including the benefit of being in CP when not using it it is .89). This strategy increases the correlation of the carry trade with both the initial TAA model and the momentum strategy. The increased correlation with the momentum strategy is due to the large influence of currency movements on the carry trade. Interestingly enough, the worst declines in this strategy have been when the market in general goes down (like in 1987 and 1998). However, the momentum strategy does not have the same volatility or exposure to what happens in the equity markets.

The momentum strategy is basically the same as the TAA strategy. I bought currencies above their 10 month MA and stayed in dollars when not in a foreign currency. However, due to the nature of the currency markets, except by hedging, you can never really have no exposure. If I bought euros and converted them to dollars, I'm effectively taking a position in dollars even though it is my home currency. The benefit of this strategy is that I'm always receiving an interest rate, it is either the dollar interest rate or a foreign one, and unless I lever this strategy, I don't necessarily have to borrow in any of them (unlike the carry trade). Anyway, this strategy has a return of about 11.4% with a standard deviation of about 6.6% with practically no correlation to the timing strategy.

Based on the returns and correlations of the two currency strategies, (and between only these two), I originally thought I should allocate about 70-80% of the currency strategy to the carry trade since that is where the Sharpe ratio is greatest for those two strategies. However, that isn't what happens in the context of the entire portfolio. Since the carry trade has greater correlation with the components of the timing model, the Sharpe ratio in an equally weighted TAA portfolio including currencies is maximized when the carry trade has no weight in the currency strategy. Giving this strategy equal weight in the TAA strategy* since April of 1980 would have decreased returns from 12.4% (with std of 6.42%) to 12.3% (with std of 5.5%) and increased the Sharpe ratio from about 1 to 1.14. Giving the currencies double or triple weight would increase the Sharpe ratio further. Even a triple weight on the currency momentum strategy will only reduce the returns by about 20 basis points historically and drops the standard deviation down below 5. Not sure yet the effect on leveraged portfolios, but that is my next step.

Since it was effective to include currencies in the TAA strategy and it is essentially a way to invest in cash, I wondered if it should it be included as the default cash strategy (eg. when the TAA model goes to cash, should it invest in currencies instead)?

Well, that answer is no. Despite the fact that the model outperforms cash with little correlation to TAA, it still will go with the market in the worst periods when the TAA strategy in general should be in cash. However, the cash returns (esp. standard deviation) do not take into account the depreciation of the dollar. All in all, it would probably be a wash and better to just keep the strategy separate, but it might be interesting to test after including the effect of depreciation (and volatility!) of the dollar.

* To be clear, what is tested is using the 10 month strategy on the countries and then investing in that as BH strategy itself. Additionally applying the 10 month strategy to the currency strategy does improve returns and Sharpe ratios for the currency strategy, but does not improve the Sharpe ratio for the overall strategy for some reason. I tested this as an afterthought, but I never wanted to test that as an original strategy, the 10 month MA is already applied individually and it makes little sense to complicate things further, IMO.

Tactical Margin Overlay

I recently posted to try to improve on my probit model by tactically adjusting margin, but it appears that there was an error in my calculation and the results are not as good as I had posted.

However, if you fade my previous results, that will tend to be have a stronger Sharpe ratio. In other words, my previous results were that you could increase your Sharpe ratio by increasing leverage when the model is in more assets. The new results are that you can increase the Sharpe ratio relative to what you would have had otherwise by increasing leverage when you're supposed to be in few assets. In the original results, the risk-parity portfolio underperformed since you were using more leverage on assets like bonds, but in this case the risk-parity portfolio performs much better. The 50% margin portfolio that uses 0 leverage when in 4 or 5 asset classes and 100% leverage in 1 or 2 asset classes has a .0364 better Sharpe ratio in the risk parity portfolio (.012 for equal weighting). Some of the cost of leverage can be made up, but the excellent returns I originally posted are not the case. Unless I combine the probit model with this model and the results are impressive, I would prefer to stick with the original model without leverage rather than these.

Another Post regarding recessions and TAA

I previously posted regarding the connection between returns of a TAA portfolio and when a recession occurs. This follow up with discuss the methodology and results from adjusting an investment strategy based on a quantitative estimate of the future probability of a recession.

The TAA models are good at reducing risk, but to increase return to something comparable to an equity index it seems silly to use the same amount of margin at all times. The post above gives evidence that lowering the amount of leverage in times when there is a prediction of a U.S. recession will increase the Sharpe ratio relative to a similarly levered model.

To incorporate this insight into the TAA model, as I used the same probit modeled I discussed in the first post I made regarding probit models. To use this model in an investing environment, I used a warm-up period of 200 months and then estimated the model each month to get a probability of a recession 12 months out. Since the NBER doesn't have dates for recessions in the past two years (I guestimated), I stopped the model 24 months prior to the end of February and used the coefficients as of that date with the data available to get the remaining predictions. Using this data I created two possible ways to scale in and out for leverage. I looked back four months for predictions in both cases. I did this for three reasons: the data constantly gets revised, I'm not sure always what is available on any given date and I want to be safe, and the lag time seems optimal (12 keeps you unlevered during the rebound, 1 is too sensitive, 6 works just as well, but I wanted to keep it shorter). So looking back four months, the first method will lever the portfolio when the estimated probability is greater than 50% and not lever the portfolio below that. The second method is similar except it provides three baskets levering a full amount, 50% of the full amount and none at all.

The results for the first and second method are comparable, but the second method slightly underperforms the first on a Sharpe ratio basis (the return is lower and the standard deviation is lower, but not by enough to offset the return). It's possible to fiddle with the parameters to improve the results, I'd rather just ignore it for the simplicity of the first model. The chart below gives the portfolio statistics for the first model with 0 leverage (and no probit data), 50% leverage, and 100% leverage. The first two columns are the base 0% and 50% and the probit columns represent the model with dynamic leverage ratios. Similar to before, I report the evenly weighted portfolios and the risk parity portfolios.

The results confirm my original intuition(!) and then the models even outperform what I had suspected would happen. Essentially the model reduces your leverage heading into a recession and then quickly puts it back on. Surprisingly, comparing these returns with the raw results from the last post on TAA and probits, shows an even better return for this method using the model than reducing leverage when a recession happened. I do use domestic equity volatility as a factor in the model which could help the investor get out when volatility increases (it is a small component compared to interest rates and money supply data though). Anyway, the results show an increase of the 50% leveraged portfolio's Sharpe ratio by almost .1 by reducing standard deviation substantially and keeping the returns constant. The 50% portfolio, previously with a horrible Sharpe ratio relative to the 0%, now is roughly comparable (with equal and risk parity weights). With 100% leverage, the risk parity probit model now has a Sharpe ratio equivalent to the equal weight 0% and 50% equal weight portfolios (but with more return and risk). However, the 100% leveraged probit models dramatically outperform their cousins without the probit model. Again, this is due to substantially reducing volatility by reducing leverage in periods leading up to recessions.

Given the success of the probit model in reducing volatility and keeping returns high, I now plan to investigate leverage as a function of the volatility of each asset class (individually). I'm guessing there would be similar results, but without some of the messier complications of using the probit model (not sure when data is released and it's relatively intensive computationally). Assuming I can find daily data from the site I got the monthly data, it shouldn't be that much of a problem and I can just use the percentage of large up and down days in a quarter as a proxy for volatility of each asset class.

A Preliminary Post regarding recessions and TAA

I was hoping to incorporate my recession model into decisions about margin into the TAA model previously blogged about (here and here), but things got away from me. The model is in Matlab and output recession predictions based on the information available at the time which was the big challenge so it really won’t be that much work beyond that. Hopefully, I can post that information tomorrow, but today I wanted to just give a brief update on the returns of the even Asset Allocation (20% in US stocks, Foreign Stocks, commodities, bonds, and REITs) vs. the returns of the Tactical version during times of recession.

I regressed the returns of the TAA strategy and the returns of the 50% levered TAA strategy against the returns on the comparable AA strategy (unlevered or levered) and a binary variable equal to 0 if the economy is not in a recession and 1 if the economy is in a recession. I’m saving the reader the time of reviewing the results, but the AA returns are highly significant (as expected) and the coefficient on the binary variable is not significant at the 5% level, but is at the 10% level for both levered and unlevered. I’m willing to concede that the effect on the adjusted R squared of the binary variable is very small, but the important thing is the sign of the coefficient and not necessarily how much of the variation is explained.

In both versions, the coefficient on the AA variable is roughly .61, but the intercept and the coefficient on the binary variable are roughly .003 and .004 in the unlevered and levered versions, respectively. These numbers are based on monthly returns, the annualized numbers are roughly 3.5% and 5%. For those without a statistical background, that means that in CAPM terms, the alpha is positive and larger for the levered version and, more importantly, both models outperform the passive strategies during recessions by a statistically and economically significant margin.

I tried to alternative strategies that could be considered a middle road. I developed two new returns variables based on the TAA data, the first was the unlevered TAA returns when there was no recession and levered otherwise and vice versa for the second. Looking at the regression results for these two gives evidence of being able to target which coefficient will be higher. Avoiding leverage in a recession increases the intercept to .004 and keeps the other coefficient flat, but avoiding leverage unless in a recession keeps the intercept, but the coefficient on the binary variable goes up to .004. Which is more important and why does it matter?

Ultimately looking at the return characteristics (below) yields the answer. As expected, the TAA model has the best Sharpe ratio; however, by avoiding margin during times of recession, you can increase the Sharpe ratio relative to a similarly leveraged portfolio. I haven’t been sure if I calculate the margin returns properly. Intuitively you would think that it would be double the returns minus the cost of debt, but with the TAA model you only margin the positions that you are in since the cost of margin is greater than the cost of cash. Furthermore, there are historical periods where the broker’s call rate gets so insanely large that it wouldn’t make sense to use margin, but this model, at present times, still uses it.

To conclude, by using a model that can predict recessions (which I conveniently have), you can improve the Sharpe ratio of leveraged portfolios. One possible note is that my model works to predict a recession within the next 12 months. It begins to show indications several months prior to a recession with plenty of time to take some off. Unfortunately this also means that there are several different ways to test it. Finally, I suspect that controlling the use of margin based on expected returns of the portfolio will also prove to enhance returns.

Component Tactical Asset Allocation: Part 3

This is the final of three posts on Tactical Asset Allocation. Part 1. Part 2.

The subject of this post is the theory of the market process and tactical asset allocation and why I believe that the former implies the latter will be a more successful strategy than buying and holding index funds.

The fundamental implication of the Efficient Markets hypothesis is that if information will be quickly incorporated in security prices. Mathematically this implies that stocks follow a random walk with jumps when new is absorbed by the market. Based on this assumption, the ideal investment strategy under the Capital Asset Pricing Model is to hold the market portfolio for the long-term (I know I’m ignoring Treynor-Black).

Beyond the typical objections to EMH, there are two main insights from the market process school that leads me to reject the EMH and I believe they are the most important observations of the school.

First, there are significant government interventions that make the market remarkably inefficient. The most important is the business cycle and monetary problems that in the 20^th century has almost always been caused by central banking. The standard Mises-Hayek theory of the business cycle is that by pushing the interest rates lower than the natural rate of interest, a central bank encourages investment beyond what would happen in the free market. Eventually the investment works its way into a boom for the producers of consumers’ goods and prices begin to increase. In order to stop the boom (to prevent runaway inflation), the central bank must raise rates. This action ends the boom and the process to correct the malinvestments made in the boom period. Since capital intensive industries are more exposed to interest rates, they typically feel more pain than consumers’ goods industries.

Moreover, governments intervene in other ways that are frequently not understood well enough by investors or they don’t always understand the implications. Economics is not a terribly difficult discipline and figuring out the implications of dumb government policies isn’t that difficult. If the government subsidizes ethanol production, farmers will use less land for the production of the typical agricultural products and those prices will have to rise. If there is a war in the Middle East, it is likely that oil (unless they have refineries in the country in question) and defense stocks will typically increase in value. Investors react in the short-term, but over the course of 6 months to a year or longer, these plays are still profitable. I’m not sure whether it is the uncertainty of these situations or that investors systemically do not think the government is as bad as it is (possible given the state of business school economics courses, also it is very difficult to quantitatively test), but investors do not react strongly enough.

Second, the market process school emphasizes the role of the entrepreneur in moving the market to equilibrium prices. EMH doesn’t care about why prices behave in certain ways, it merely attempts to model them. However, what is seen as a random walk are actually deliberate actions taken by entrepreneurs engaging in speculation and arbitrage. Entrepreneurs who have greater foresight will outperform those who don’t. Furthermore, the investing, particularly derivatives, are referred to as zero-sum games. The profits are zero-sum; however, ex ante, all of these trades are positive sum in terms of utility. These trades show ex post profits or losses depending on the skill in forecasting of the entrepreneur.

Finally, as Hayek notes, there’s no such thing as perfect knowledge, as is assumed by the actors in CAPM. Knowledge is dispersed throughout society and the purpose of the market is to organize that knowledge. Market prices reflect the knowledge of all market participants.

Combined these three factors make tactical asset allocation an attractive prospect. Since there are cycles that can be observed by students of the Austrian School, it makes little sense to buy and hold equities when there are lengthy periods of time where you can lose a significant sum of money. Also, not only is there a purpose to being an entrepreneur which is ignored in the EMH, but paying attention to what happens to prices can reveal knowledge about other market participants’ knowledge and opinions in the market. Michael Covel notes in his book about trend following that trend followers tend not to be in the business of predicting trends, they have imperfect knowledge and as a group they have no opinions on the market. However, if the market is going up, they would be more than happy to buy and vice versa to sell. The logic is essentially the same for TAA. Mr. Faber isn’t providing a service in predicting the market, he’s trying to improve on the buy and hold passive strategy by staying out of the market when market participants have a negative outlook. Nothing wrong with that.

Component Tactical Asset Allocation: Part 2

This is the continuation to the previous Component TAA: Part 1 post.

First I will present the results with a single momentum strategy comparing the AA, TAA, and Momentum TAA strategies with 0 leverage and with 2-1 leverage. Then, I will present alternate momentum strategies using different js and ks, but investing in a constant number of ETFs followed by a constant j and k with a different % of ETFs available. I will conclude with work in progress to improve it further. I might add an additional post describing why the economist in me prefers Tactical Asset Allocation as an investment philosophy to the Efficient Markets Hypothesis and the Capital Asset Pricing Model.

Before I begin, I should note that the Domestic ETFs I invest in a separated into two groups, sector and style. Whichever one I can invest in earlier (sector), I will use that return and then later, I average the two's returns. I might get a better return without doing this, but that particular market is so broad that I wanted to investigate the combined effect. Not only do some sectors out perform, but sometimes value outperforms growth and large-cap outperforms small-cap. I wanted to be able to include this relationship as well, I'm just not sure how much stronger this effect is compared to the sectors. I also had a longer list of sectors that I cut down on prior to running these returns, so the ranking since I updated the data can actually choose from more sectors and gets better returns. I'm only reporting a sector basket with the 9 Spider select ETFs.

The first table represents a unlevered comparison of the AA, TAA, and Momentum TAA (with j=4 and k=2 investing in the ETFs ranking in the top 25%) with equal asset allocation between the 5 asset classes and the Risk Parity weights discussed in the previous part. The TAA beats the AA which is the conclusion reached by Faber. However, the Sharpe Ratio (@ 6% for all) increases with a more normal kurtosis (3=normal, greater than 3 indicates fat tails) by using the risk parity weights. There are similar results comparing the TAA and Momentum TAA, however it seems like the Kurosis for the TAA portfolio is relatively constant. This makes sense since the data is cut off prior to 1998 and excludes some of the larger price movements.


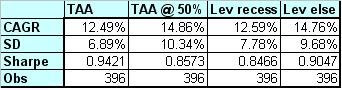
The next table is the same strategies and comparison as above, but with 100% leverage. It is more for general interest than comparison. The method used in the paper by Panagora was to use the Risk Parity weight and then lever the portfolio to a desired return (such as the S&P500's average return) so that variance would be minimized. In this case, the return on the TAA without Risk Parity Weights would be greater than the standard deviation on something like the S&P500. You could use roughly 20% leverage to increase the return of the TAA Risk Parity to roughly the return on the normal TAA (this same argument works to target the standard deviation as well). However, the Sharpe ratio in this case would be less than if you had not used leveraged. The return is the same, but the variance is actually greater (the same holds true for AA, TAA, and Momentum TAA). So even without the large 2-1 leverage reported below, if you measure your investment success by your Sharpe ratio, then it won't make sense to use leverage. However, relatively speaking, the risk parity weights outperform the equal weighted portfolio. If you're an investor seeking to maximize profit or would be willing to accept more risk in exchange, then you should use the risk parity instead of the equal weight portfolios.



The third table presents the CAGR, Standard Deviation, and Sharpe Ratio comparing different momentum strategies. Recall from the previous article that j represents the number of periods to look back to and k represents the number of periods to hold (since k can be greater than 1, then even if you hold 6 ETFs when k=1, it will be variable for k>1). Using more complete data, it is clear that the Sharpe Ratios increase as j comes to 3 or 4 and declines after that. However, there is no clear trend on what happens with k. It usually increases to 2 and declines after that, but it is not consistent. If at all possible, I would prefer a larger k to a smaller k since it guarantees that I will have less turnover.



Finally, the last table shows the returns with j=4 and k=2, but investing in a different percentage of the ETFs that have sufficient return histories. The trend in this case is clear, return increases as you increase the percentage until it tops out between 25 and 33.3%. However, these returns are all gross and the others could relatively increase if transactions costs are included. Furthermore, I would suspect the tax consequences are greater. Instead of picking the best sectors, at 75% you're getting out of the worst. For portfolios with less than half a million dollars, there might be too many ETFs to be able to use the 75% or 50% to make it worth it. However, I should also note that the benefit of the original TAA model is that each position can be approximated with futures contracts which could possibly reduce costs and provide an easier method to use leverage.



To conclude, gross returns and gross Sharpe ratios are greater using the Momentum TAA with risk parity portfolios. However, there are still additional ways that it could be improved. This strategy can be considered a component in a larger overall strategy. For example, Mr. Faber discusses alternative strategies such as mean reversion and following hedge fund managers that produce significant returns. I think that there are strategies in options, distressed debt, value investing, macro investing, mean reversion, and statistical arbitrage (or investing in hedge funds that specialize in stat, risk, or convertible arb) that can add to this return while not being correlated with the TAA or Momentum TAA. Unfortunately, with the exception of mean reversion, these strategies are either not quantitative (macro, distressed debt, value) or are difficult to backtest (options - competence, and arbitrage are arbitraged away).

Next, there are additional beta factors that can be considered or thought about in different ways. For example, a recent paper indicates that the returns for currency managers are largely Beta. Those returns could be an additional asset class that could be added with little correlation to the others. Also, there is evidence that investing in commodities based on their term structure (buy most backwardated positive roll-return commodities, short most negative roll-return contango commodities). These two strategies, combined with mean reversion of the five assets used in TAA and the Momentum TAA risk parity weights, could be particularly strong and they could be included in a broader portfolio using the risk parity weights.

Finally, I recently discussed a probit model I use to forecast recessions. I am considering linking that model (and augh converting it to Matlab) to this program so that I choose margin based on the probability of a recession. The returns of this strategy outperform the S&P500 during the bad times, but they still underperform compared to the remainder of the period. I'm going to consider increasing leverage when the probability estimates are low and cut off leverage when the probability begins to increase. I believe this can improve returns.

edit: There was a slight discrepancy with the interest rate data in the original results that has been corrected.

On to Part 3.

Component Tactical Asset Allocation: Part 1

Mebane Faber published an article in the Journal of Wealth Management in the Spring of 2007 called a Quantitative Approach to Tactical Asset Allocation. The thrust of the paper is that if you invest in U.S. stocks, foreign stocks, bonds, commodities, and REITs when they are above their respective 200 day moving averages and invest in commercial paper otherwise, you can achieve returns similar to equity investments with significantly lower volatility. Mr. Faber has graciously provided the monthly returns from the strategy as well as much more information on his website, World Beta. Based on the data on the website (more up to date than the original paper), the timing model returned 12% since 1972 with a standard deviation of 6.43% (.93 Sharpe) compared to an 11.5% return on the buy and hold asset allocation strategy (20% in each asset mentioned above) with a 9.78% standard deviation (.56 Sharpe). I programmed his strategy into Matlab using the same data and found similar results (slightly different due to the vagaries of Matlab rounding and computing returns statistics based on monthly data instead of yearly data).

Lately I have been interested in how to improve on this concept. First, I would like to discuss two additions I made and I will make an additional post to discuss the results of what I tested.

On his blog, Mr. Faber compares different methods that readers have requested to improve the returns (that he doesn't use). The first is to enter long positions above the 200 day MA and short positions below while the second is to enter each position "all in," equally weighted for each buy signal, no positions in cash . Each of these methods fails to improve the Sharpe ratio. I expect the L/S portfolio fails due to the fact on that most of the top 50 best and worst days are when the market is below the 200 day moving average. It is possible to profit by shorting the worst, but you can get burned on the best.

I believe the "all in" portfolio fails by ignoring the correlations between the assets (and would require more re-balancing costs than the traditional TAA). In order to test this, I followed a white paper by Panagora Research which describes the Risk Parity Portfolio. Their concept is to adjust the weights of a portfolio so that the amount you can risk on each position is equal. The traditional method to do this is to estimate the Value at Risk for a portfolio and break it into the component parts for each security. This method takes into account the correlations among each asset and the Beta. As a technical concern, I waited a year to create the Risk Parity weights (but used the initial 20% allocation during that period to make comparisons to Faber's paper) and brute forced the first weights using the covariance matrix and existed at the time of investment decisions and only changed the weights if the Component Value at Risk of an individual asset went outside predefined bounds. The weights stay relatively constant over time, but I could have created tighter bounds where they would change more often. As of the time of writing, bonds would have 34.8% weight, REITs 15.9%, Commodities 19.3%, Domestic Stocks 15.1%, Foreign Stocks 14.9%. In other words, REITs and Stocks would have their shares reduced and bonds would increase their weights in order to take into account the fact that they are more strongly correlated with each other than Commodities and Bonds and have higher variances. Based on the research provided by Panagora, I expected a slightly lower return, but a substantially reduced standard deviation.

The other method I used was investigating the j-k Momentum strategy proposed by Jegadeesh and Titman. In this paper, J and T investigate ranking stocks based on their returns from j periods ago and holding them for k periods forward. They used this model to show that stocks have a momentum factor like a size or value factor that helps determine their future returns. Within the context of the TAA model, I chose to test this strategy by choosing a proportion of the ETFs for an asset class and then applying the j, k methodology to a proportion of the ETFs with returns. I waited until a certain proportion of the total ETFs (in each classand that I considered representative of the asset class) began to trade to start the momentum strategy for that asset class. I will only report (and compare) the returns since the earliest strategy began to take effect (Select Spiders began trading in December of 1998, but it requires j months before the strategy can work). Since they have uneven start times, I used the returns from the normal TAA strategy when the Momentum strategy cannot work. I should emphasize that I am not using only a Momentum strategy on ETFs, but investing in a j-k Momentum strategy based on a TAA model. Within each Momentum category, the ETFs are equally weighted and I don't think it makes sense to use Risk Parity Portfolios in this context.

Furthermore, if I am not mistaken, Mr. Faber uses a method similar to this in actual practice, however, he does not report his results using this method. The most obvious reason is that he created his model in Excel which is substantially more cumbersome the model gets more complex. Also, ETFs have a short history that may not be indicative of the 35 years of returns where the TAA model has shown considerable strength. There's also no doubt that using ETFs in this strategy would require more trading costs and more taxes (unless in a tax-free account). Even if this strategy is not successful (it is), it is at least interesting to investigate and note the return characteristics for different levels of j and k.

The next post will compare the Equal Allocation (no TAA) model to the TAA and their Risk Parity equivalent portfolios, it will compare the TAA models with the Momentum TAA models (equal allocation and risk weighted), and some discussion about future additions I plan on testing.

On to Part 2.