I was hoping to incorporate my recession model into decisions about margin into the TAA model previously blogged about (here and here), but things got away from me. The model is in Matlab and output recession predictions based on the information available at the time which was the big challenge so it really won’t be that much work beyond that. Hopefully, I can post that information tomorrow, but today I wanted to just give a brief update on the returns of the even Asset Allocation (20% in US stocks, Foreign Stocks, commodities, bonds, and REITs) vs. the returns of the Tactical version during times of recession.
I regressed the returns of the TAA strategy and the returns of the 50% levered TAA strategy against the returns on the comparable AA strategy (unlevered or levered) and a binary variable equal to 0 if the economy is not in a recession and 1 if the economy is in a recession. I’m saving the reader the time of reviewing the results, but the AA returns are highly significant (as expected) and the coefficient on the binary variable is not significant at the 5% level, but is at the 10% level for both levered and unlevered. I’m willing to concede that the effect on the adjusted R squared of the binary variable is very small, but the important thing is the sign of the coefficient and not necessarily how much of the variation is explained.
In both versions, the coefficient on the AA variable is roughly .61, but the intercept and the coefficient on the binary variable are roughly .003 and .004 in the unlevered and levered versions, respectively. These numbers are based on monthly returns, the annualized numbers are roughly 3.5% and 5%. For those without a statistical background, that means that in CAPM terms, the alpha is positive and larger for the levered version and, more importantly, both models outperform the passive strategies during recessions by a statistically and economically significant margin.
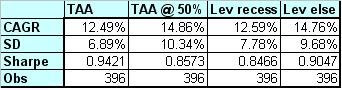
I tried to alternative strategies that could be considered a middle road. I developed two new returns variables based on the TAA data, the first was the unlevered TAA returns when there was no recession and levered otherwise and vice versa for the second. Looking at the regression results for these two gives evidence of being able to target which coefficient will be higher. Avoiding leverage in a recession increases the intercept to .004 and keeps the other coefficient flat, but avoiding leverage unless in a recession keeps the intercept, but the coefficient on the binary variable goes up to .004. Which is more important and why does it matter?
Ultimately looking at the return characteristics (below) yields the answer. As expected, the TAA model has the best Sharpe ratio; however, by avoiding margin during times of recession, you can increase the Sharpe ratio relative to a similarly leveraged portfolio. I haven’t been sure if I calculate the margin returns properly. Intuitively you would think that it would be double the returns minus the cost of debt, but with the TAA model you only margin the positions that you are in since the cost of margin is greater than the cost of cash. Furthermore, there are historical periods where the broker’s call rate gets so insanely large that it wouldn’t make sense to use margin, but this model, at present times, still uses it.
To conclude, by using a model that can predict recessions (which I conveniently have), you can improve the Sharpe ratio of leveraged portfolios. One possible note is that my model works to predict a recession within the next 12 months. It begins to show indications several months prior to a recession with plenty of time to take some off. Unfortunately this also means that there are several different ways to test it. Finally, I suspect that controlling the use of margin based on expected returns of the portfolio will also prove to enhance returns.
No comments:
Post a Comment