Wednesday, April 30, 2008
Here's for not understanding GDP numbers
If you go into table 2.3.1 (or 2.3.6), you will see why services are strong. Basically, in spite of a housing recession, spending on housing (services, not to be confused with residential investment) goes up. I'm not surprised that housing operation is going up (electricity is increasing at a 15% rate), but I'm a little baffled why in the middle of dramatic decreases in home prices and sales that spending on housing would be increasing. Medical care and household operation (electricity mostly) make up a big percentage of the increase in services (and therefore services), roughly half. And another large increase is due to other. The big question I have is, why isn't spending on housing services decreasing in the GDP numbers rather than consistently increasing? The durable goods section showed only a small decrease, but the average increase since 2006 in the housing services number has been .6% and increased by .55% this time. Effectively in line. Granted that the ISM non-manufacturing index was below 50 the entire quarter, it makes even less sense why services would be increasing.
Ultimately, if you use better inflation numbers or per-capita figures, this would probably be the second quarter of a declining GDP. Not the best definition of whether we are in a recession, but it's what the financial press usually talks up.
Wednesday, April 23, 2008
Long-term Component Timing Model
The general strategy is as simple as the TAA strategy. If the subindex is above 10month SMA, invest, otherwise stay in commercial paper. For equities, I also entered the entire asset class in CP when the broad index is below the SMA. They have much stronger correlation to the index than the other asset classes. Asset classes are equally weighted. I'll only report since 1991 (when I have data for commodities). The returns are consistent over time, they tend to slightly decrease, but with consistently lower volatility.
For reference, the AA strategy has a return of 9.65% (7.8% stdev) and the TAA is 10.8% (6% stdev). Extending the strategy with the component timing model gives 10.4% (4.7% stdev). Adding in a currency strategy similar to this* will reduce returns to 9.9% (4.2%).
*including interest rates from holding foreign currencies, but not counting the movements of currencies when in domestic currency since other asset classes do not control for value of the dollar which makes it not comparable to past strategies, all this does it lower the return and keeps volatility relatively constant, just wanted to be conservative
For the unlevered strategies, the alpha of each strategy is highly significant (<.01%) at 3% (.64 Beta) for the original, 3.6% (.46 Beta) timing w/o currencies, and 3.2% (.42 Beta) with currencies. The alpha of the timing (w/o curr) vs. the TAA strategy is significant at 1.7%. Using 2:1 leverage (except for the currencies), the TAA strategy has an alpha 4.86% (1.2 Beta), 6.3% (.92 Beta) timing w/o currencies, and 5.4% (.8 Beta) with currencies. Note that the levered returns are 16.1% (12% stdev) for the TAA, 15.6% (9.4% stdev) for the timing w/o currencies, and 14.3% (8.1% stdev) with currencies. Using even more leverage (1.5x), would give an even larger return for the timing model with roughly the volatility of the 2:1 TAA strategy.
Note that I did not use a momentum strategy, just the timing model. This means that there would be relatively small transaction costs, but you could not use futures contracts to implement it (except commodities and foreign indices). Nevertheless, it shows that there is significant evidence that this strategy has worked over a significant period of time with a variety of asset classes. I expected the returns to be different since I am using more equally weighted portfolios than cap-weighted as the indices are (within each it is cap, between each it is equal), but I was pleasantly surprised at how well it performed over the past 18 years or so (and 30 years) which gives further evidence that the momentum strategy for the component TAA strategy or a strategy like this with much less in trading costs.
Tuesday, April 22, 2008
Value Investing
Wednesday, April 16, 2008
Commodities and Countries Update
* 50% decreases the Sharpe of the foreign strategy by themselves, but increases the Sharpe of the OVERALL strategy, I just wanted to be consistent with previous posts
addendum: I should note that the returns to this strategy are over a long period of time, particularly since the currency strategy benefits from high interest rates. The Sharpe ratios come down significantly over the past ten years compared to the past thirty years. Since the strategy has maintained a more constant growth path (ie not the early/mid 80s), the country strategy improves the Sharpe from .83 to .96 for the TAA strategy (individual country TAA is .93). However, the inclusion of the currency strategy has a smaller effect (I don't take into account the declining value of the dollar on any assets besides currencies, so this could be understated) increasing the Sharpe ratio by .04-.05. It seems that compared to the 50% momentum strategy over the past ten years, the EAFE has outperformed historically so that the momentum strategy is relatively constant, but the EAFE outperforms. (.4 10 year Sharpe vs. .1 30 year) in the past few years. I'm not sure how long the EAFE will continue to outperform, but I would prefer the less volatile Sharpe ratio. Right now my thinking is that after taking into account the depreciation of all of these assets in dollar terms, the best cash strategy would be the currency strategy, but I'm not sure yet.
Not impressed with JPM
Of course Wall Street cares more about coming in line with estimates than actual figures (EPS down 50% yoy, 20% qoq, "could have been worse, buy"). However, if you actually look at the 8-K instead of looking at the headline number, you would notice that JPMorgan made about a billion dollars on the Visa deal. The Corporate/PE division had 1.027 billion in net income which is actually 72 if you subtract out the Visa deal. I don't expect them to make any one-time deals with this much profit over the next year so I would guess that the next earnings will come out much lower than this quarter's. I would expect the remaining quarters to be closer to an average of last year's profit for this division and then a rosy estimate would be that the other divisions keep net income constant (or growing/declining at the rates from Q4 to Q1, effectively flat overall). In this case, Net Income would be 600 million lower (assuming same level of credit losses which I really have no way to estimate, could be lower could be higher and would have a big effect on Net Income) or at 1.8 billion. That would put a crude estimate of EPS for next quarter at .50 or down about 25% qoq (or similarly for this quarter assuming the IBanking revenue was not above average and down 43% qoq from that perspective).
These are crude assumptions, but an exceptional one-time event like the largest IPO in history should not be the saving grace during the credit crunch. I care about earnings going forward.
Note: WFC actually does have a pretty good business model. Over 90% of their loans are prime. They're going to lose some money, but be in a much better position coming out of this crisis. All of their business segments showed declining yoy, but that will likely turn around better than other banks.
JPM is still up .75% from the open (10:20).
Tuesday, April 15, 2008
Commodities and Foreign Countries
I'll start with the GSCI. I used data available from the Global Financial Database on Commodities futures since 1983 (except Natty Gas which is since 1990). Unfortunately, they didn't have all of the energy contracts and were missing a few of the other contracts. I kept each commodity subgroup (livestock, ag, energy, ind. metals, precious metals) the same weight and scaled up the components. I confirmed that this index has about a 94% correlation with the GSCI. I was a little disappointed with this figure (preferring higher than 97.5%), but I will make due with what I have. I tested just performing the timing on the sectors (since 91) and on the individual components (since 83). One thing is very clear, the GSCI is dominated by energy you cannot compare an equally weighted TAA strategy with the market-weighted portfolio in GSCI. If you compare the strategies, use weights close to GSCI.
With sectors and a buy and hold strategy, my returns are initially different than the GSCI, so I don't expect the best comparison for the timing, but with 94% correlation, I would expect similar trends. However, I found that the return/sd ratio increased for the GSCI strategy, but not the component strategy. Variance decreased, but returns decreased as well and the effect was not economically significant. On the other hand, the returns to the GSCI strategy are enhanced considerably. The returns and correlations are roughly the same if you break it down into all of the contracts weighted by what is in GSCI. I wouldn't be surprised if some of this result is due to the fact that many of these commodities contracts show considerable seasonal variation that cannot be reduced easily by using the 200 day MA the way that an equity indices returns are improved (they lack the seasonal variations) and that the aggregate figure trends better. A more complex strategy, such as taking advantage of contango or backwardation, might be more appropriate for the components of the GSCI. There are other indices that I could use to test this method since I didn't have all the contracts (I will use the CRB indices except energy which I will have to recreate).
Countries, on the other hand, do trend well and the timing strategy works very well on them. I used total return data and replicated the EAFE index since 1994 with a 99% correlation. Before that time period, I replaced the FTSE-100 with the All-Shares index and some other total return indices are used that don't have futures contracts for them.
(begin digression: I had to use alternative indices for some countries that didn't have total return indices for the whole period, however, the question is how the strategy improves on this Buy and Hold strategy and not necessarily on the EAFE. If it improves returns over a long period of time, you could reasonably assume that it would continue to outperform in the future with futures contracts available and that the returns that you have are highly correlated with what you would have had with futures contracts. The returns are probably slightly better since the indices used are all-share instead of focused, but you would also expect the variance to be higher, it is equivalent to using the Wilshire 5000 instead of S&P500: end digression).
I also didn't use all of the indices in the EAFE since some of them have very small weights and the countries don't have actively traded futures. The top 12 or so are good enough. In general the equal weighted strategy outperforms the EAFE weights (due to the 25% weight on Japan). The difference isn't large enough to concern ourselves about over the long-term (1.26 CAGR/STD vs. 1.25). Over the long-term, the buy and hold returns were different between the EAFE and weighing the individual components (since there are times when I don't have France or Singapore's total return indices), but again the comparison I want to make is between the trends and not the absolute levels. From 1970 to February of this year, the Buy and Hold for the EAFE had a CAGR/std ratio of .715 (CAGR=11.7%) and the component strategy was .82 (CAGR=13.1%). Overlaying the timing strategy increased the Sharpe ratio on the EAFE to .99 (CAGR=12.4%) and the component to 1.25 while increasing the return to 13.6%. Since 1988 (when I have data on France), the spread between the strategies has stayed strong although overall returns aren't as strong. The Buy and Hold on EAFE went from .43 to .64 and with the component strategy it went from .62 to .95.
The 6% Sharpe ratio of the original TAA strategy was about 1.0 (12.4% CAGR) since April of 1980 and 1.14 (12.3% CAGR) with a currencies strategy. Replacing the EAFE increases the Sharpe to roughly 1.04 (12.5% CAGR) in the original and 1.18 (12.4% CAGR). The excess returns show an insignificant alpha over the original TAA strategy, but with the currency strategy included there is a significant alpha of 30 bps which reduces to about 25 bps when currencies have a 3x weight (Sharpe of 1.31 vs. 1.27 originally).
Also note that this is a timing model just like the one before. There isn't the excessive trading costs of a momentum strategy. You would be in each country about 60-75% of the time and frequently for years at a time. Someone with a large account could use this strategy to help reduce risk while keeping returns constant (meaning more leverage could be used).
Monday, April 14, 2008
The Simon Hypothesis and Investing
That is an empirical question, but I think most people's first hunches would be that it would be impossible to predict. I would argue that this much is true for many walks of life, particularly investing. We might know the ant's final destination ahead of time (or the subprime crisis, or the internet bubble to burst), but how we get to that conclusion would be different every time. So while a backtested strategy might look sound on paper, ultimately, there is no way to tell if the path which reached a destination in the past will reach the destination in the future. The most important aspect of long-term investing is thinking about why the fundamental economic reasons why the strategy should earn abnormal returns in the future (if you can't think of any good ones, put your money in index funds and T-Bills). In the TAA case, I believe it takes advantage of the boom/busts inherent in markets (with central banks). A deep value investor or distressed debt investor survives through their entrepreneurial foresight (much more important to the Austrians than the neoclassicals which could be one reason why they don't teach value investing with a tenth the attention payed to CAPM), and so forth.
I guess the key insight is that you need to be flexible. You're not sure where the path can take you, so you should always try to find the shortest route when you can. You're never sure what surprises can force you to take twice as long a route, but in markets like this, it isn't hard (WB, BSC,ABK, WM,etc).
Sunday, April 13, 2008
Currency Strategies
There are four main sources of currency beta: value, momentum, carry, and volatility. Value is described as the PPP strategy, taking advantage of relative differences in long-term reversals to the mean of currencies with overvalued or undervalued currencies (on the basis on inflation and interest rates). Momentum is a trend-following strategy. Carry is investing in high interest rate countries and borrowing in low interest rate countries. A volatility strategy uses options on currencies and would be more exotic than a retail investor would want to use (and is most likely used to take into account exotic strategies a hedge fund manager uses and show that they are most likely just long/short volatility).
Well, I have been interesting in including the Beta of currencies in tactical asset allocation portfolios (see here for original post) and I wanted to experiment with these strategies. I generally am skeptical of the mean-reversion strategy since I've seen the charts of countries deviating from PPP estimates for decades. It's too hard to compare a basket of consumption goods between the countries to measure PPP accurately enough for me to be confident enough to invest using it. Volatility would also be too difficult to test and I've never traded currency options. It might be something to add in the future, but I'm guessing that strategy is too volatile for me...
So I set my eyes on the carry and momentum strategies. The carry strategy is particularly interesting to me since there already is an ETF which does that for you. DBV goes long the highest yielding currencies and short the lowest yielding ones to profit from the spread of the interest rates so long as exchange rates do not move very far. I replicated the strategy using all of the currencies that the ETF uses (and before the Euro I used France and Germany) going back to 1980 (when I could get decent interest rate data for some of the smaller countries). I replicated the DBV strategy as best as I could, except that I had to use some alternative interest rate data with longer histories instead of Libor (and then I continued to use that instead of switching to the country's interbank rates after the interbank data becomes available). I got a 95% correlation with the DBV since it has been in existence with a 10% return with a 7.8% standard deviation since 2000 (however, they report a cumulative return of 518% (14.67% annualized) since inception and I only showed 354% (8.5%), not sure how they account for the Euro, this could be the reason why). It's not perfect, but it's good enough (mine is crude since it may not always be market neutral b/c I'm lazy and don't plan to use it to invest with)
Taking the strategy further back (to 1980), there was a smaller return 6.3% (with 9% std) which could be attributable to wider (or more volatile) interest rate spreads during the 1980s which converged to roughly .4% in recent years. Ultimately the strategy has a very low correlation with the timing strategy that's been developed here and at WorldBeta and with the momentum strategy I will detail below. Also, based on my crude analysis, applying a 10 month moving average to this strategy increases the return:risk ratio from .694 to 1.15 (without including the benefit of being in CP when not using it it is .89). This strategy increases the correlation of the carry trade with both the initial TAA model and the momentum strategy. The increased correlation with the momentum strategy is due to the large influence of currency movements on the carry trade. Interestingly enough, the worst declines in this strategy have been when the market in general goes down (like in 1987 and 1998). However, the momentum strategy does not have the same volatility or exposure to what happens in the equity markets.
The momentum strategy is basically the same as the TAA strategy. I bought currencies above their 10 month MA and stayed in dollars when not in a foreign currency. However, due to the nature of the currency markets, except by hedging, you can never really have no exposure. If I bought euros and converted them to dollars, I'm effectively taking a position in dollars even though it is my home currency. The benefit of this strategy is that I'm always receiving an interest rate, it is either the dollar interest rate or a foreign one, and unless I lever this strategy, I don't necessarily have to borrow in any of them (unlike the carry trade). Anyway, this strategy has a return of about 11.4% with a standard deviation of about 6.6% with practically no correlation to the timing strategy.
Based on the returns and correlations of the two currency strategies, (and between only these two), I originally thought I should allocate about 70-80% of the currency strategy to the carry trade since that is where the Sharpe ratio is greatest for those two strategies. However, that isn't what happens in the context of the entire portfolio. Since the carry trade has greater correlation with the components of the timing model, the Sharpe ratio in an equally weighted TAA portfolio including currencies is maximized when the carry trade has no weight in the currency strategy. Giving this strategy equal weight in the TAA strategy* since April of 1980 would have decreased returns from 12.4% (with std of 6.42%) to 12.3% (with std of 5.5%) and increased the Sharpe ratio from about 1 to 1.14. Giving the currencies double or triple weight would increase the Sharpe ratio further. Even a triple weight on the currency momentum strategy will only reduce the returns by about 20 basis points historically and drops the standard deviation down below 5. Not sure yet the effect on leveraged portfolios, but that is my next step.
Since it was effective to include currencies in the TAA strategy and it is essentially a way to invest in cash, I wondered if it should it be included as the default cash strategy (eg. when the TAA model goes to cash, should it invest in currencies instead)?
Well, that answer is no. Despite the fact that the model outperforms cash with little correlation to TAA, it still will go with the market in the worst periods when the TAA strategy in general should be in cash. However, the cash returns (esp. standard deviation) do not take into account the depreciation of the dollar. All in all, it would probably be a wash and better to just keep the strategy separate, but it might be interesting to test after including the effect of depreciation (and volatility!) of the dollar.
* To be clear, what is tested is using the 10 month strategy on the countries and then investing in that as BH strategy itself. Additionally applying the 10 month strategy to the currency strategy does improve returns and Sharpe ratios for the currency strategy, but does not improve the Sharpe ratio for the overall strategy for some reason. I tested this as an afterthought, but I never wanted to test that as an original strategy, the 10 month MA is already applied individually and it makes little sense to complicate things further, IMO.
Friday, April 11, 2008
Checking your assumptions
I've been researching strategies for currencies and adding them to the Tactical Asset Allocation strategy (here). This strategy is already very successful so I was surprised to find out how good a simple currency momentum strategy was when added to the portfolio. I didn't realize at first how important it was to check the assumptions regarding the data. I downloaded the data from the St. Louis Fred website and it was monthly data, I assumed it would be fine. The problem was that the data isn't end of the month data, it is the average of a month's daily data. This is a good thing for running regressions with exchange rates or using them to adjust accounting information, but it's not good for trading strategies. Even creating new month time series with the end of the month or middle of the month dates will dramatically underperform the average series (Global Financial Database has the numbers based on end of month which I will be using in the future). You can only know the average rate for the month at the end of the month so by assuming you get out at the average rate you're assuming that you know the entire month's returns sometime that is not the end of the month.
I originally performed this research by looking at several different currencies until I realized what I did wrong, but it is easier to illustrate with one currency.
Just to illustrate how far off it is, using the strategy (L/S 2 period MA timing) on the Pound going back to 72 (including interest rates), will give a return of about 15.6% (8.1% std) on the average of the month data, 9.64% (10.3% std) on the end of the month data, and 12.4% (9.7% std) on the middle of the month data. The best thing about the strategy is that it has virtually 0 correlation with the TAA model (why it deserves such a huge weight in it originally) using any of the datapoints. That alone leads me to believe that currencies should have a position in a well-diversified portfolio. With the British pound strategy as a proxy for how well the complete momentum (it isn't, but I suspect that strategy will be better), the Sharpe ratio will be increasing with a positive weight on the currency strategy until about 40% (for the middle of month, 25% for end of month). I'm comparing it with the basic TAA model with equal weights on the remaining assets. I can only guess that the well-diversified currency strategy will perform even better and should receive a larger allocation.
To test this without compiling all of the interest rate data and combining everything (next project: recreate the carry trade) I tested a j=4, k=2 momentum strategy on the currency ETFs that are available since September of 2006. This is a very short time frame when all of these ETFs performed very well, but it would represent at least the long-side of the strategy accurately. The strategy would be in either two or three currency ETFs and has a CAGR of 13.8% with a 5.6% standard deviation. I would reiterate again that this is a period of a massive decline in the dollar and it is not expected that this kind of risk:return ratio would continue in the future (the return is expected more than the risk). Over this time period, the strategy (absolute returns) has a correlation with the TAA model of 19%. 19% isn't 0, but it still should be important enough to add to the portfolio after completing a more rigorous long-term examination of the strategy.
Wednesday, April 9, 2008
Tactical Margin Overlay
However, if you fade my previous results, that will tend to be have a stronger Sharpe ratio. In other words, my previous results were that you could increase your Sharpe ratio by increasing leverage when the model is in more assets. The new results are that you can increase the Sharpe ratio relative to what you would have had otherwise by increasing leverage when you're supposed to be in few assets. In the original results, the risk-parity portfolio underperformed since you were using more leverage on assets like bonds, but in this case the risk-parity portfolio performs much better. The 50% margin portfolio that uses 0 leverage when in 4 or 5 asset classes and 100% leverage in 1 or 2 asset classes has a .0364 better Sharpe ratio in the risk parity portfolio (.012 for equal weighting). Some of the cost of leverage can be made up, but the excellent returns I originally posted are not the case. Unless I combine the probit model with this model and the results are impressive, I would prefer to stick with the original model without leverage rather than these.
Tuesday, April 8, 2008
Momentum Average and TAA
The results were as I expected. The momentum strategy isn't that good more than six months out and averaging the good Sharpe strategy with the bad Sharpe strategy really doesn't improve the returns. Intermediate trends are strong enough for ETFs that that should be the focus. I was able to improve on his idea by changing it to an average of 1 month, 3 month, and 4 month returns and the 1 month and 4 month are an improvement still above the momentum average. They still don't outperform the j=4, k=2 model in backtests, but they could outperform other models and there's no reason why it can't outperform in the future. The two bottom strategies at least relieve some of the burden on the 4 month.

I should also note that I am continually refining these strategies including the calculation of interest, margin, and the risk parity weights. I'll always post a comparison to a base model whenever it is different from anything posted in the past. The difference in returns from this model to the original reflects better accounting of interest returns. I also took out the previous inclusion of the style ETFs. Sector momentum has previously been far more important than style momentum and I expect that to continue in the future.
Friday, April 4, 2008
Another Post regarding recessions and TAA
The TAA models are good at reducing risk, but to increase return to something comparable to an equity index it seems silly to use the same amount of margin at all times. The post above gives evidence that lowering the amount of leverage in times when there is a prediction of a U.S. recession will increase the Sharpe ratio relative to a similarly levered model.
To incorporate this insight into the TAA model, as I used the same probit modeled I discussed in the first post I made regarding probit models. To use this model in an investing environment, I used a warm-up period of 200 months and then estimated the model each month to get a probability of a recession 12 months out. Since the NBER doesn't have dates for recessions in the past two years (I guestimated), I stopped the model 24 months prior to the end of February and used the coefficients as of that date with the data available to get the remaining predictions. Using this data I created two possible ways to scale in and out for leverage. I looked back four months for predictions in both cases. I did this for three reasons: the data constantly gets revised, I'm not sure always what is available on any given date and I want to be safe, and the lag time seems optimal (12 keeps you unlevered during the rebound, 1 is too sensitive, 6 works just as well, but I wanted to keep it shorter). So looking back four months, the first method will lever the portfolio when the estimated probability is greater than 50% and not lever the portfolio below that. The second method is similar except it provides three baskets levering a full amount, 50% of the full amount and none at all.
The results for the first and second method are comparable, but the second method slightly underperforms the first on a Sharpe ratio basis (the return is lower and the standard deviation is lower, but not by enough to offset the return). It's possible to fiddle with the parameters to improve the results, I'd rather just ignore it for the simplicity of the first model. The chart below gives the portfolio statistics for the first model with 0 leverage (and no probit data), 50% leverage, and 100% leverage. The first two columns are the base 0% and 50% and the probit columns represent the model with dynamic leverage ratios. Similar to before, I report the evenly weighted portfolios and the risk parity portfolios.

The results confirm my original intuition(!) and then the models even outperform what I had suspected would happen. Essentially the model reduces your leverage heading into a recession and then quickly puts it back on. Surprisingly, comparing these returns with the raw results from the last post on TAA and probits, shows an even better return for this method using the model than reducing leverage when a recession happened. I do use domestic equity volatility as a factor in the model which could help the investor get out when volatility increases (it is a small component compared to interest rates and money supply data though). Anyway, the results show an increase of the 50% leveraged portfolio's Sharpe ratio by almost .1 by reducing standard deviation substantially and keeping the returns constant. The 50% portfolio, previously with a horrible Sharpe ratio relative to the 0%, now is roughly comparable (with equal and risk parity weights). With 100% leverage, the risk parity probit model now has a Sharpe ratio equivalent to the equal weight 0% and 50% equal weight portfolios (but with more return and risk). However, the 100% leveraged probit models dramatically outperform their cousins without the probit model. Again, this is due to substantially reducing volatility by reducing leverage in periods leading up to recessions.
Given the success of the probit model in reducing volatility and keeping returns high, I now plan to investigate leverage as a function of the volatility of each asset class (individually). I'm guessing there would be similar results, but without some of the messier complications of using the probit model (not sure when data is released and it's relatively intensive computationally). Assuming I can find daily data from the site I got the monthly data, it shouldn't be that much of a problem and I can just use the percentage of large up and down days in a quarter as a proxy for volatility of each asset class.
Thursday, April 3, 2008
When will an American presidential candidate talk like this?
HT: Robert Lawson
A Preliminary Post regarding recessions and TAA
I was hoping to incorporate my recession model into decisions about margin into the TAA model previously blogged about (here and here), but things got away from me. The model is in Matlab and output recession predictions based on the information available at the time which was the big challenge so it really won’t be that much work beyond that. Hopefully, I can post that information tomorrow, but today I wanted to just give a brief update on the returns of the even Asset Allocation (20% in US stocks, Foreign Stocks, commodities, bonds, and REITs) vs. the returns of the Tactical version during times of recession.
I regressed the returns of the TAA strategy and the returns of the 50% levered TAA strategy against the returns on the comparable AA strategy (unlevered or levered) and a binary variable equal to 0 if the economy is not in a recession and 1 if the economy is in a recession. I’m saving the reader the time of reviewing the results, but the AA returns are highly significant (as expected) and the coefficient on the binary variable is not significant at the 5% level, but is at the 10% level for both levered and unlevered. I’m willing to concede that the effect on the adjusted R squared of the binary variable is very small, but the important thing is the sign of the coefficient and not necessarily how much of the variation is explained.
In both versions, the coefficient on the AA variable is roughly .61, but the intercept and the coefficient on the binary variable are roughly .003 and .004 in the unlevered and levered versions, respectively. These numbers are based on monthly returns, the annualized numbers are roughly 3.5% and 5%. For those without a statistical background, that means that in CAPM terms, the alpha is positive and larger for the levered version and, more importantly, both models outperform the passive strategies during recessions by a statistically and economically significant margin.
I tried to alternative strategies that could be considered a middle road. I developed two new returns variables based on the TAA data, the first was the unlevered TAA returns when there was no recession and levered otherwise and vice versa for the second. Looking at the regression results for these two gives evidence of being able to target which coefficient will be higher. Avoiding leverage in a recession increases the intercept to .004 and keeps the other coefficient flat, but avoiding leverage unless in a recession keeps the intercept, but the coefficient on the binary variable goes up to .004. Which is more important and why does it matter?
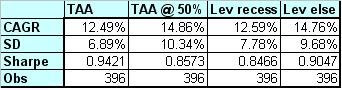
Ultimately looking at the return characteristics (below) yields the answer. As expected, the TAA model has the best Sharpe ratio; however, by avoiding margin during times of recession, you can increase the Sharpe ratio relative to a similarly leveraged portfolio. I haven’t been sure if I calculate the margin returns properly. Intuitively you would think that it would be double the returns minus the cost of debt, but with the TAA model you only margin the positions that you are in since the cost of margin is greater than the cost of cash. Furthermore, there are historical periods where the broker’s call rate gets so insanely large that it wouldn’t make sense to use margin, but this model, at present times, still uses it.
To conclude, by using a model that can predict recessions (which I conveniently have), you can improve the Sharpe ratio of leveraged portfolios. One possible note is that my model works to predict a recession within the next 12 months. It begins to show indications several months prior to a recession with plenty of time to take some off. Unfortunately this also means that there are several different ways to test it. Finally, I suspect that controlling the use of margin based on expected returns of the portfolio will also prove to enhance returns.